CHAPTER - 6

MACROMECHANICAL BEHAVIOUR

6.1 INTRODUCTION

6.2 THREE-DIMENSIONAL MATERIAL ANISOTROPY

6.3 MATERIAL SYMMETRY

6.4 ELASTIC CONSTANTS AND COMPLIANCES IN TERMS OF  ENGINEERING CONSTANTS

6.5 CYLINDRICAL ORTHOTROPY

6.6 TWO-DIMENSIONAL CASE: PLANE STRESS

6.7 TRANSFORMATION OF ELASTIC CONSTANTS AND COMPLIANCES

    6.7.1 Three-Dimensional Case

    6.7.2 Two-Dimensional Case

6.8 PARTICULATE AND SHORT FIBRE COMPOSITES

6.9 MULTIDIRECTIONAL FIBRE REINFORCED COMPOSITES

6.10 UNIDIRECTIONAL LAMINA

6.11 BIDIRECTIONAL LAMINA

6.12 GENERAL LAMINATES

6.13 LAMINATE HYGROTHERMAL STRAINS

6.14 STRENGTH CRITERIA FOR ORTHOTROPIC LAMINA

6.15 BIBLIOGTAPHY

6.16 EXERCISES

6.1 INTRODUCTION

            The heterogeneity in a composite material is introduced due to not only its bi-phase or in some cases multi-phase composition, but also laminations. This leads to a distinctly different stress strain behaviour in the case of laminates. The anisotropy caused due to fibre orientations and the resulting extension-shear and bending-twisting coupling as well as the extension-bending coupling developed due to unsymmetric lamination add to the complexities. A clear understanding of the constitutive equations of a composite laminate is thus desirable before these are used in analysis and design of composite structures. In this chapter, we first introduce to the readers the basic constitutive equations for a general three-dimensional anisotropic material with and without material symmetry, elastic constants and compliances and their relations to engineering constants, as well as transformation laws for elastic constants and compliances for both three and two-dimensional cases. We also discuss constitutive relations for several composite materials–particulate and short fibre composites, multidirectional fibre reinforced composites, unidirectional lamina and general laminates as well as lamina strength criteria.

6.2 THREE-DIMENSIONAL MATERIAL ANISOTROPY

            For a three-dimensional elastic anisotropic body (Fig. 6.1), the generalized Hook's law is expressed as

                             (i, j = 1,2,3)                                         (6.1)

where  and  are the stress and strain tensors, respectively, and  are the elastic constants. Here the indices i, j, k and l can assume values of 1, 2 and 3. This implies that there may exist 3⁴ = 81 independent elastic constants. However, it is known from the theory of elasticity, that both stress tensor  and strain tensor  are symmetric. As = ,  =

and as  = ,  =                                                                      (6.2)

Thus,  =  =  =                                                                   (6.3)

            This results in reduction of possible independent elastic constants to thirty-six.

            Further, if there exists a strain energy U such that

                                                                                            (6.4)

with the property that , then

 =                                                                                                       (6.5)

 Equation 6.5 in conjunction with Eq. 6.3 finally reduce the total number of independent elastic constants from thirty-six to twenty-one only. Such an anisotropic material with twenty-one independent elastic constants is termed as triclinic. Now, using the following contracted single index notations

                                                 (6.6)

the constitutive relations for the general case of material anisotropy are expressed as

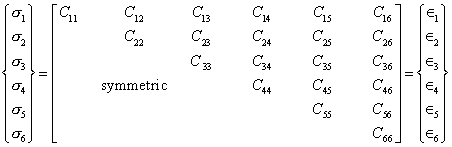                   (6.7)

or,       ;        i, j = 1, 2,….,6                                                             (6.8)

Here, [ ] is the elastic constant matrix.

Conversely, {  } = [S_ij ] {} ;        i, j =1, 2,…..,6                                                (6.9)

where [S_ij] is the compliance matrix.

Note that

[S_ij] = [C_ij ]^-1                                                                                                    (6.10)

Also,    [ ] =[ ] and [S_ij] = [S_ji] due to symmetry.

6.3 MATERIAL SYMMETRY

            There may exist several situations when the distribution and orientation of reinforcements may give rise to special cases of material property symmetry. When there is one plane of material property symmetry (say, the plane of symmetry is x_{3 =} 0, i.e., the rotation of 180 degree around the x₃ axis yields an equivalent material), the elastic constant matrix [ ] is modified as

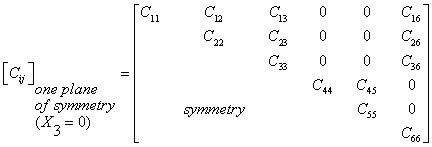            (6.11)

Thus there are thirteen independent elastic constants, and the material is monoclinic. The compliance matrix [S_ij] for a monoclinic material may accordingly be written from Eq. 6.11 by replacing 'C ' with 'S '.

            If there are three mutually orthogonal planes of symmetry, the material behaviour is orthotropic. The elastic constant matrix  is then expressed as

_orthotropic =                         (6.12)

Thus there are nine independent elastic constants. Correspondingly there exist nine independent compliances.

            Two special cases of symmetry, square symmetry and hexagonal symmetry, may arise due to packing of fibres in some regular fashion. This results in further reduction of independent elastic constant. For instance, if the fibres are packed in a square array (Fig. 6.2) in the X₂X₃ plane. Then

[]

_{square array} =                    (6.13)

There exist now six independent elastic constants. Similarly, when the fibres are packed in hexagonal array (Fig. 6.3),

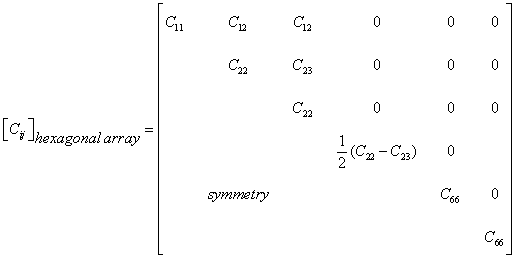
                                                                                                                                                               (6.14)

In the case of hexagonal symmetry, the number of independent elastic constants is reduced to five only. The material symmetry equivalent to the hexagonal symmetry, is also achieved, if the fibres are packed in a random fashion (Fig. 6.4) in the X₂X₃ plane. This form of symmetry is usually termed as transverse isotropy. The [ ] matrix due to the transverse isotropy is the same as that given in Eq. 6.14. The compliance matrices corresponding to Eqs. 6.12 through 6.14 can be accordingly written down. However,it may be noted that in the case of rectangular array (Fig. 6.5), C₁₂ ≠ C₁₃, C₂₂ ≠ C₃₃ and C₅₅ ≠ C₆₆ (Eq. 6.13).

Material Isotropy

            The material properties remain independent of directional change for an isotropic material. The elastic constant matrix [ ] for a three dimensional isotropic material are expressed as

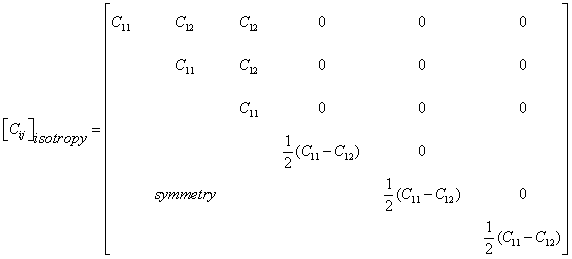
                                                                                                                                                                      (6.15)

The compliance matrix [S_ij] for an isotropic material can be accordingly derived.

6.4 ELASTIC CONSTANTS AND COMPLIANCES IN TERMS OF

      ENGINEERING CONSTANTS

            The elastic constants or compliances are essentially material constants. Incidentally, the determination of all these elastic constants or compliances is not easy to accomplish by simple tests. The material constants that are normally determined through characterization experiments (see chapter 4) are termed as engineering constants. They can also be evaluated using the micromechanics material models (chapter 5).

            All nine independent compliances and therefore elastic constants listed in Eq. 6.12 are now expressed in terms of nine independent engineering constants. The stress-strain relations for a three-dimensional orthotropic material, in terms of engineering constants, can be written as follows:

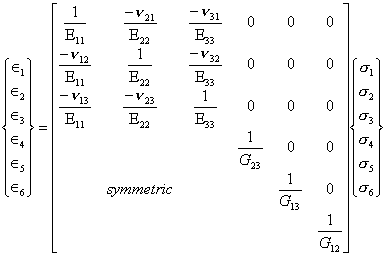                       (6.16)

We know that, in terms of compliances, the stress-strain relations are

                                                                            (6.17)

Comparing Eqs. 6.16 and 6.17, we can express the compliances in terms of engineering constants.

                                                                             (6.18)

            The elastic constants can then be derived by inversion of the compliance matrix i.e. [] = [S_ij]^-1 and are given as follows:

                                                                                   (6.19)

where

             (6.20)

In terms of engineering constants, the elastic constants and compliances for an isotropic material are given by      

                                                                (6.21)

and               

6.5 CYLINDRICAL ORTHOTROPY

            Consider cylindrical coordinates r, θ, z as illustrated in Fig. 6.6. Here the z-axis is assumed to coincide with the X₃-axis. The stress and strain components are represented as

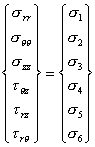                     and 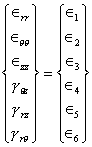                                                          (6.22)

The stress-strain relations, in terms of compliances, become

                                         (6.23)

where

                                                                             (6.24)

     The elastic constant matrix [] is obtained by inversion of the compliance matrix [S_ij] i.e., [] = [S_ij]^-1 or from Eq. 6.19 by replacing the indices 1,2,3 with r, θ, z respectively.

6.6 TWO-DIMENSIONAL CASE: PLANE STRESS

For the case of plane stress (Fig. 6.7)

            σ₃ = σ₄ = σ₅ = 0                                                                                                (6.25)

            The stress-strain relations, with two-dimensional anisotropy, are

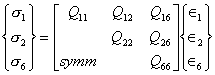                                                                              (6.26)

or,                 i, j = 1,2,6                                                                   (6.27)

Where [Q_ij] are the reduced stiffnesses (elastic constants) for plane stress.

Similarly, in terms of compliances, the stress-strain relations are

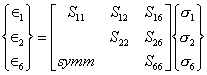                                                                                            (6.28)

or,                 i, j =1,2,6                                                                    (6.29)

            For the case of two-dimensional orthotropy (Fig. 6.8) the stress-strain relations are

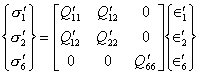                                                                                  (6.30)

and

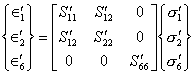                                                                                   (6.31)

with

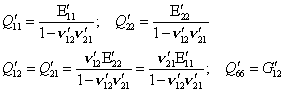                                                             (6.32)

and

                                 (6.33)

            Note that the engineering constants , , , (or ) and G'₁₂ are referred to the orthotropic axis system X'₁X'₂ (i.e., the material axes).

6.7 TRANSFORMATION OF ELASTIC CONSTANTS AND COMPLIANCES

            If the elastic constants and compliances of a material are known with respect to a given co-ordinate system, then the corresponding values with respect to any other mutually perpendicular coordinates can be determined using laws of transformation. These are explained in Appendix A.

6.7.1 Three-Dimensional Case

            The transformation of elastic constants from the X'₁X'₂X'₃ coordinates to mutually orthogonal X₁X₂ X₃ coordinates (Refer Fig. A.1 and Eq. A. 22) is given as follows:

                                                                                                   (6.34)

where transformation matrix  is given by Eq. A.8.

Note that the elements of and  correspond to the X₁X₂ X₃ and X'₁X'₂X'₃ coordinates, respectively.   

            One can use Eq. 6.34 in the following form

           = ^{-T  -1}

                    = [T_σ] [T_σ]^T                                                                                      (6.35)

if the transformation is required from X₁X₂ X₃ coordinates to theX'₁X'₂X'₃ coordinates. Note that [T_σ] is defined by Eq. A.13.

Simalarly,

                                                                                                  (6.36)

                                                                                                   (6.37)

            The corresponding elastic constants and compliances [S_ij] due to special cases of material symmetry and transformation matrices  and [T_σ] due to specific orientation of axes are to be reduced from the general three dimensional cases, before transformation is sought from one axis system to the other.

6.7.2 Two-Dimensional Case

            If the elements of  and  refer to the X₁X₂ and X'₁X'₂ coordinates (see Eqs. 6.26 and 6.30 and Figs. 6.7 and 6.8), respectively, then transformation laws for reduced elastic constants are obtained as follows:

                                                                                                  (6.38)

                                                                                                 (6.39)

where  and are defined by Eqs. A.18 and A.19. The compliance matrices are accordingly transformed using Eqs. 6.36 and 6.37.

            Accordingly, from Eqs. 6.38 and A.18 it can be shown that

                       (6.40)

In a similar way from Eqs. 6,36 and A.19 one obtains

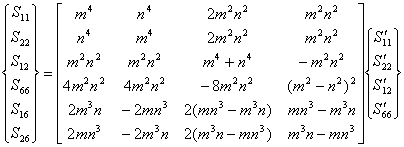                   (6.41)

Note that m = cos  and n = sin and  and  are defined by Eqs. 6.32 and 6.33 respectively, in terms of engineering constants , ,  (or ) and G'₁₂ corresponding to principal material directions.

            If transformation is required from one anisotropic material axis system (say X₁X₂ X₃) to another anisotropic material axis system (say, ), then from Eqs. 6.38 and A. 18 we can

or,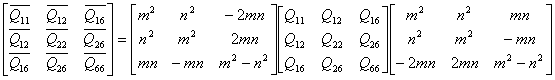           

or,

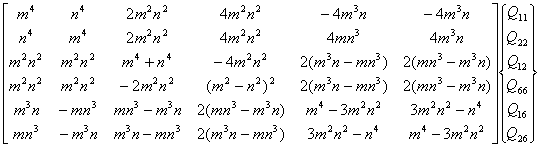
                                                                                                                                    (6.42)

Similarly, using Eqs. 6.36 and A.19 one can write

or,

                                                                                                                                    (6.43)

6.8 PARTICULATE AND SHORT FIBRE COMPOSITES

            Particulate composites, where reinforcements are in the form of particles, platelets and flakes, and short fibre composites may exhibit a wide range of elastic material behaviour depending on the shapes, sizes, orientations and distributions of reinforcements in the matrix phase as well as elastic properties of the constituent materials. The matrix behaviour is normally isotropic. The composition of these composites are first established by examining their morphology and then proper stress-strain relations can be obtained from the equations developed in the preceding sections. It is also to be noted whether the composite body under consideration is three-dimensional or two dimensional in character.

            For example, the behaviour of a three-dimensional composite with a typical reinforcement packing shown in Fig. 6.9a is anisotropic in nature. Here the reinforcements are oriented in some regular fashion with respect to the reference axes X₁X₂ X₃. The stress strain relations  = for this type of composites are given by Eq 6.8 with elements of  listed in Eq. 6.7. When the reinforcements are arranged parallel to the axes (Fig. 6.9b), the composite behaviour is orthotropic and Eq. 6.12 defines the corresponding . If the orientation and distribution of reinforcements are found to be random in the matrix phase, as shown in Fig. 6.9c, the composite is assumed to behave like an isotropic material. Consequently, the elastic constant matrix  is reduced to that given in Eq. 6.15.

            For two-dimensional anisotropic, orthotropic and isotropic cases, some possible reinforcement arrangements are illustrated in Fig. 6.10. The stress-strain relations, as presented in section 6.6 can be accordingly used for these cases.

            If transformations of elastic constants and compliances are required from one axes system to another, then one can use the transformation rules discussed in section 6.7.

Fig. 6.10

6.9 MULTIDIRECTIONAL FIBRE REINFORCED COMPOSITES

            Composites exhibit strong directional properties, when reinforcements are in the form of continuous fibres. In a multidirectional composite, fibres can be placed in any desired direction in a three-dimensional space, along which better stiffness (or strength) is desired. The shear properties can be greatly improved by providing diagonal reinforcements. Carbon-carbon composites form an important class of multidirectional composites due to several variations in weave design and perform construction. Similar multi-directional composite systems can also be designed and developed with both metal-matrix and ceramic-matrix composites. A typical multi-directional (5D) composite is shown in Fig. 6.11a. There are three bundles of orthogonal fibres f₁, f₂, f₃ and two bundles of diagonal fibres f₄, f₅. We consider here an integrated multidirectional fibre reinforced composite moder which contains n number of unidirectional fibre composite blocks that are oriented in n arbitrary directions with respect to a three-dimensional reference axes X₁X₂ X₃. Each unit block may have different fobre volume fractions. This arrangement makes n number of material axis systems, and therefore yield n sets of direction cosines between n material axis systems and the reference axes X₁X₂ X₃. For example, Figure 6.11b represents the orientation of the material axis system for the ith block. The corresponding transformation matrices and  can then be written down using Eqs. A.8 and A.13, respectively.

            The material behaviour for each block with respect to its axes is orthotropic. The elastic constants for the ith block are then given as

                                                 (6.44)

The effective elastic constants for the n-directional fibre reinforced composite are then determined by averaging the transformed properties as follows:

                                                                                      (6.45)

Note that the overall fibre volume fraction is given as

                                                                                                          (6.46)

6.10 UNIDIRECTIONAL LAMINA

            A unidirectional lamina is a thin layer (ply) of composite and is normally treated as a two-dimensional problem. It contains parallel, continuous fibres and provides extremely high directional properties. It is the basic building unit of a laminate and finds very wide applications in composite structures specially in the form of laminates. Therefore, the knowledge of its elastic macromechanical behaviour is of utmost importance to composite structural designers.

            Figure 6.12a depicts a unidirectional lamina where parallel, continuous fibres, are aligned along the X'₁ axis (fibre axis or longitudinal direction). The X'₂ axis (transverse direction) is normal the fibre axis. The axes X'₁X'₂ are referred as material axes. The material axes are oriented counter clockwise by angle  with respect to the reference axes X₁X₂. The angle  (also referred as fibre angle) is considered positive when measured counterclockwise from the X₁ axis. This type of unidirectional lamina is termed as “off-axis” lamina. An off-axis lamina behaves like an anisotropic two-dimensional body, and the stress-strain relations, given by Eqs. 6.26 through 6.29, can be used for the present case.

            When the material axes coincide with the reference axes (i.e., =0), as shown in Fig. 6.12b, the lamina is termed as “on-axis” lamina and its behaviour is orthotropic in nature. The stress-strain relations are defined by Eqs. 6.30 and 6.31.

            The engineering constants , , , (or ) and G'₁₂ are usually known, as these can be determined either by using micromechanics theories (chapter 4) or by characterization tests (chapter 5). Using these engineering constants, the reduced stiffnesses and compliances  are then determined for an orthotropic lamina with the help of Eqs. 6.32 and 6.33. The transformed reduced stiffnesses and can now be evaluated employing Eqs. 6.40 and 6.41. The stiffness  and compliances for three composite systems are computed for various fibre orientations and are listed in Tables 6.1 and 6.2. Typical variations of transformed properties  and  with change in the fibre angle  are illustrated in Figs. 6.13 and 6.14. Such plots aid to the basic understanding of the stiffness behaviour of an off-axis lamina with different fibre orientations. Note that the case =0 corresponds to an on-axis lamina.

6.11 BIDIRECTIONAL LAMINA

6.12 GENERAL LAMINATES

            We consider here a general thin laminate of thickness h (Fig. 6.16). The X₃ axis is replaced here by the z axis for convenience. The laminate consists of n number of unidirectional and/or bidirectional laminae, where each lamina may be of different materials and thicknesses and have different fibre orientations (). A thin general laminate is essentially a two-dimensional problem, but cannot be treated as a two-dimensional plane stress problem as has been done for a unidirectional lamina. The existence of extension –bending couling causes bending, even if the laminate is subjected to inplane loads only. Therefore, thin plate bending theories are employed in derivation of constitutive relations. We assume that Kirchhoff 's assumptions related to the thin plate bending theory are applicable in the present case.

            Let u₁⁰, u₂⁰ and w are the mid-plane displacements, and w is constant through the thickness of the lamina. Then the mid-plane strains are given by

                                                                   (6.47)

and the curvatures, which are constant through the thickness of the laminate, are

                                           (6.48)

            The strains at any distance z are then given as

                                    (6.49)

            Now from Eq. 6.26, we have at any distance z

                                                                        (6.50)

            The stress and moment resultants (Fig. 6.17) are evaluated per unit length of the laminate as follows:

             and                                             (6.51)

Thus,

where  and

where  

Proceeding in a similar manner, all stress and moment resultants can be expressed as listed below:

                                                   (6.52)

with (A_ij, B_ij, D_ij) = _ij (1, z, z²) dz;             i, j = 1, 2, 6                                          (6.53)

            Equation 6.52 represents the constitutive relations for a general laminate, and A_ij, B_ij, and D_ij are the inplane, extension bending coupling and bending stiffnesses, respectively. Note that all these stiffnesses are derived for a unit length of the laminate. The elastic properties of each lamina are generally assumed to be constant through its thickness, as these laminae are considered to be thin. Then A_ij, B_ij, and D_ij are approximated as

From Eq. 6.52, it is seen that there exist several types of mechanical coupling in a general laminate. These are grouped together as follows:

            Extension – Shear                     :   A₁₆, A₂₆

            Extension – Bending                 :   B₁₁, B₁₂, B₂₂

                Extension – Twisting                 :   B₁₆ , B₂₆

            Shear – Bending                       :    B₁₆ , B₂₆

                Shear – Twisting                       :     B₆₆

            Bending – Twisting                   :     D₁₆ , D₂₆

            Biaxial – Extension                    :     A₁₂

            Biaxial – Bending                      :     D₁₂

As stated earlier, the coupling terms B_ij occur due to unsymmetry about the middle surface of a laminate. However, all terms containing suffices '16 ' and '26 ' are resulted due to anisotropy caused by the fibre orientation  other than 0⁰ and 90⁰. Those containing suffices '12 ' are due to Poisson's effect. Although a heneral unsymmetric laminate contains all coupling terms, there are several laminates where some of these may vanish. These are listed in Table 6.3. There are several important points that are to be noted here. The first two laminates (serial nos. 1 and 2) which are christened as “off-axis laminate” and “on-axis laminate”; respectively are essentially paralles ply laminates where all laminae in a laminate have the same fibre orientation and therefore are stacked parallel to each other. These are, in fact, similar to unidirectional laminae. For a symmetric balanced angle-ply laminate D₁₆ and D₂₆ do not vanish, although A₁₆ = A₂₆ = 0. The only coupling effect that appears in an anti-symmetric cross-ply laminate is the extension-bending coupling due to presence of B₁₁and B₂₂ and note that B₂₂ = - B₁₁. But the existence of B₁₆ and B₂₆ cause an antisymmetric angle-ply laminate to experience extension-twisting coupling. Note also that extension-bending coupling is predominant for an unsymmetric cross-ply laminate.

            The mechanical coupling, as discussed above, influences the deformation behaviour of a laminate to a great extent. This can be better understood by examining the deformed shapes of a couple of laminates as illustrated in Figs. 6.18 through 6.20. Here the dotted lines represent the undeformed shape and the firm lines, deformed shapes. Consider first a simple off-axis laminate (or unidirectional lamina), subjected to an inplane stress resultant N₁ (Fig.6.18a) and an out-of-plane moment resultant M₁ (Fig. 6.18b). We know from Eq. 6.52 and Table 6.1 (B_ij=0) that

                                                                                     (6.55)

Thus, as illustrated in Fig. 6.18a, it is noted that a simple tension causes not only extension and contraction, but also shearing of the laminate. While the extension and contraction are due to A₁₁ and A₁₂, respectively and the inplane shear deformation is due to presence of A₁₆. This characteristic behaviour is seen especially in an anisotropic (off-axis) laminate. The shear deformation vanishes, if A₁₆ = 0, as in the case of an orthotropic (on-axis) laminate (serial no.2 of Table 6.1). Similarly, as can be seen in Fig. 6.18b, a simple bending due to M₁ has resulted not only longitudinal bending (due to D₁₁) and transverse bending (due to D₁₂), but also twisting (due to D₁₆).

            Figure 6.19 describes the deformation behaviour of an antisymmetric cross-ply laminate. The extension-bending coupling due to B₁₁ and B₂₂ can be clearly observed. In Fig. 6.19a a simple inplane tension is found to introduce bending in the laminate. Conversely, a simple bending causes extension of the laminate, a shown in Fig. 6.19b.

            Figure 6.20 depicts the deformed shape of an antisymmetric angle-ply laminate. Here the extension-bending and bending-shear coupling effects due to B₁₆ and B₂₆ are presented. In a similar manner, the deformation characteristics of other types of laminates can be illustrated. The most important point that is to be focused here is that fibre orientation and lamina stacking sequence affect laminate stiffness properties, which, in turn, control the deformation behaviour of a laminate.

            Table 6.4 provides the stiffnesses [A_ij], [B_ij]and [D_ij] for various stacking sequences of carbon/epoxy composites. The [Q_ij] values given in Table 6.1 have been used to compute the above stiffnesses.

            The changes in moisture concentration and temperature introduce expansional strains in each lamina. The stress-strain relation of an off-axis lamina (Eq. 6.28) is then modified as follows           

                                                           (6.56)

with

                                                                                                  (6.57)

and

                and                                                      (6.58)

where the superscripts e, H, T refer to expansion, moisture and temperature, respectively, ΔC and ΔT are the change in specific moisture concentration and temperature, respectively, and β's and α's are coefficients of moisture expansion and thermal expansion respectively.

            Note that the spatial distributions of moisture concentration and temperature are determined from solution of moisture diffusion and heat transfer problems.

            Expansional strains transform like mechanical strains (Appendix A) i.e., .

Inversion of Eq. 6.56 yields (see also Eq. 6.26), at any distance z (Fig. 6.16),            (6.59)

Thus, for a general laminate Eq. 6.52 will be modified as

                                                                                                                     (6.60)

where the expansional force resultants are

                                                                    (6.61)

and the expansional moments are

                                                              (6.62)

These expansional force resultants and moments may considerably influence the deformation behaviour of a laminate.

            Isotropic materials do not have any preferential direction and in most cases tensile strength and compressive strength are equal. The shear strength is also dependent on the tensile strength. A strength criterion for an isotropic lamina is, therefore, based on stress components, σ₁, σ₂ and σ₆ for a two-dimensional problem and a single strength constant i.e., ultimate strength X. An orthotropic lamina (Fig. 6.8), on the other hand, exhibits five independent strength constants e.g., tensile strength X'₁₁^t a dcompressive strength X'₁₁^c along the X'₁ direction; tensile strength X'₂₂^t and compressive strength X'₂₂^c along the X'₂ direction and inplane shear strength X'₁₂. Hence a strength criterion for a two-dimensional orthotropic lamina should involve the stress components σ'₁, σ'₂ and σ'₆ and strength constants X'₁₁^t, X'₁₁^c, X'₂₂^t X'₂₂^c and X^'₁₂. We present here a few important strength criteria that are commonly used to evaluate the failure of an orthotropic lamina. Maximum Stress Criterian

            A lamina is assumed to fail, if any of the following relations is satisfied

,  when  and  are tensile

, when  and  are compressive.                                 (6.63)

It is assumed that inplane shear strengths are equal under positive or negative shear load.

Maximum Strain Criterian

            A lamina fails, if any of the following is satisfied

 when  and  are tensile

 when  and  are compressive.                                  (6.64)

Note that the addition of suffix 'u' in strain components indicates the corresponding ultimate strains. The ultimate shear strains are also assumed to be equal under positive or negative shear load. If a material behaves linearly elastic till failure, the ultimate strains can be related to ultimate strength constants as follows:

                                                                   (6.65)

Tsai-Hill Criterion

            The general three-dimensional orthotropic strength criterion is given by

             (6.66)

Assuming that normal stresses ,  and  an dshear stress  act independently and substituting  = X'₁₁, = X'₂₂,  and  in the above strength criterion, we obtain

; ;                      (6.67)

Combining Eqs. 6.67 we get

                                                                     (6.68)

Assuming transverse symmetry X'₂₂ = X'₃₃  and two-dimensional plane stress case (σ₃ = σ₄ = σ₅ =0), Eq. 6.66 reduces to

or,

                                                                  (6.69)

When ,  or both are tensile or compressive, Eq. 6.69 can be used by substituting the corresponding tensile or compressive strength constants in it. Thus, if  is tensile, X'₁₁ = X'₁₁^t , and if is compressive, X'₂₂= X'₂₂^c and so on.

            Tsai-Hill/Hoffman criterion accounts for unequal tensile and compressive strengths. For a three-dimensional state of stress in an orthotropic material, this criterion is given as

               (6.70)

            If tensile  acts only and =X'₁₁^t , then from Eq. 6.70

(C₂ + C₃)  X'₁₁^t  + C₄  = 1/X'₁₁^t                                                                        (6.71)

If compressive  acts only and -= X'₁₁^c, then

           (C₂  + C₃)  X'₁₁^c – C₄ = 1/X'₁₁^c                                                             (6.72)

From Eqs. 6.71 and 6.72, we obtain

                                                                     (6.73)

Similarly, consideration of  and  yields

                                                                     (6.74)

                                                                      (6.75)

Now, assuming , we derive from the above the following relations for C₁, C₂ and C₃:

                                                                               (6.76)

                                                                                       (6.77)

Further, applying  only and  yields

                                                                                                                (6.78)  

Now, considering a two dimensional state of plane stress condition and substituting the values of C₁, C₂, C₃, C₄, C₅ and C₉ from the above relations, the strength criterion takes the following form:

           (6.79)

            For an orthotropic material under a two-dimensional state of plane stress condition, this criterion assumes the form

                                 (6.80)

Considering that the positive or negative inplane shear stress  should not affect the results, the terms F₁₆ , F₂₆ and F₆ should vanish. Hence Eq. 6.80 reduces to

                        (6.81)

Now applying independently tensile and compressive normal stresses  and , and inplane shear stresses , and substitution of =X'₁₁^t - =X'₁₁^c, =X'₂₂^t , - = X'₂₂^c and =X'₁₂ in Eq. 6.81 yields

                                                                                                  (6.82)

Employing the von Mises plane stress analogy, the remaining interaction coefficient F₁₂ can be defined

                                                                            (6.83)

Combining Eqs. 6.81-6.83, the Tsai-Wu criterian takes the following form:

                                                     (6.84)

It is to be mentioned that the Tsai-Wu criterion (Eq. 6.84) accounts for interaction of stress components as well as both tensile and compressive strength constants and shear strength and is considered as a reasonably accurate and consistent representation of failure of an orthotropic lamina under biaxial stresses. The Tsai-Hill criterion (Eq. 6.69) is also very popular with composite structural designers.

Table 6.3 : Stiffnesses for various types of laminates

 Case   Laminate type                      Elastic behaviour                            Stiffnesses

I. Symmetric Laminates

1.   Off-axis laminate                          anisotropic                             all B_ij=0;  A_ij= h Q_ij

        (all plies oriented                          and uncoupled                       D_ij = (h³/12) Q_ij

      at )

2.   On-axis laminate                          orthotropic                            all  B_ij=0;  A_ij=h Q_ij

      (all plies oriented either                and uncoupled                       and D_ij = h³/12) Q_ij

      0⁰ or 90⁰)                                                                                 with Q₁₆ = Q₂₆ = 0

3.   Symmetric cross-ply                    specially                                all B_ij=0; A₁₆= A₂₆=

      (odd number of                            orthropic and                         D₁₆= D₂₆=0; rest of

      0⁰ / 90⁰ / 0⁰, etc. plies)                 uncoupled                              A_ij and D_ij are finite

4.   Symmetric angle-ply                    anisotropic and                      all B_ij=0; all A_ij and D_ij

      (odd number of /-/,             uncoupled                              are finite

       etc. plies)

5.   Symmetric balanced angle            anisotropic and                      all B_ij=0; A₁₆= A₂₆=0 rest

      ply (/-/-/, etc. plies)         uncoupled                              of A_ij and D_ij are finite.

II. Unsymmetric Laminates

6.   Antisymmetric cross-ply               orthotropic and                      A₁₆= A₂₆= B₁₆= B₂₆=

      (even number of                           partly coupled                        B₁₂= B₆₆= D₁₆= D₂₆=0

      0⁰ / 90⁰ / 0⁰/90⁰, etc. plies)                                                        rest of A_ij ,B_ij and D_ij are

                                                                                                      finite with B₂₂=-B₁₁;

                                                                                                      D₂₂=-D₁₁

7.   Antisymmetric angle-ply               anisotropic and                      A₁₆= A₂₆=B₁₁=B₂₂

      (even number of                           partly coupled                        B₁₂= B₆₆= D₁₆= D₂₆=0

      (/-//-, etc. plies)                                                            rest of A_ij, B_ij and D_ij are   

                                                                                                      finite.

8.   Unsymmetric cross-ply                orthotropic but                       A₁₆= A₂₆= B₁₆= B₂₆=

      (irregular stacking of                    coupled                                 D₁₆= D₂₆=0; rest of

      0⁰ or 90⁰ plies)                                                                          A_ij, B_ij and D_ij are

                                                                                                      finite.

9.   General unsymmetric                    anisotropic and                      all A_ij, B_ij and D_ij are

      laminate                                       strongly coupled                    finite.

Table 6.4: Stiffneses  for carbon/epoxy composite laminates

Laminate Thickness : 4mm

Units : [A_ij], GPa-mm;                       [B_ij], GPa-mm²;                     [D_ij], GPa-mm³

1.  0⁰ / 90⁰ / 0⁰ laminates

2. 45⁰ / -45⁰ / 45⁰  laminate

3. 45⁰ /-45⁰ /45⁰ / 45⁰  laminate

4. 0⁰ /90⁰ / 0⁰ / 90⁰  laminate

5.  45⁰ /-45⁰ /45⁰ / -45⁰  laminate

6. 0⁰ /90⁰ /0⁰ / 0⁰  laminate

6.15 BIBLIOGTAPHY

1.      S.P. Timoshenko and J.N. Goodier, Theory of Elasticity, McGraw Hill, N.Y., 1970.

2.      Y.C. Fung, Foundations of Solid Mechanics, Englewood Cliffs, N.J., 1965.

3.      S.G. Lekhnitskii, Theory of Elasticity of an Anisotropic Body, MIR Publ. Moscow, 1981.

4.      J.C, Halpin, Primer or Composite Materials: Analysis, Technomic Publ. Co., Inc. Lancaste, 1984.

5.      R.M. Christensen, Mechanics of Composite Materials, Wiley Interscience, N.Y., 1979.

6.      Z. Hashin and C.T. Herakovich (Eds.), Mechanics of Composite Materials-Recent Advances, Pergamon Press, N.Y.,1983.

7.      S.W. Tsai and H.T. Hahn, Introduction to Composite Materials Technomic Publ. Co., Inc., Lancaster,1980.

8.      J.M. Whitney, Structural Analysis of Laminted Composites, Technomic Publ. Co., Inc.,Lancaster, 1987.

9.      J.R. Vinson and R.L. Sierakowski, The Behaviour of Structures Composed of Composite Materials, Kluwar Academic Publ., MA,1985.

10.  S.W. Tsai, J.C. Halpin and N.J. Pangano (Eds.) Composite Materials Workshop, Technomic Publ. Co., Inc., Lancaster, 1968.

6.16 EXERCISES

1.      State the generalized Hooke's law for a three-dimensional elastic anisotropic material and show that there are twenty-one independent elastic constants for a triclinic material.

2.      Write down the elastic constant matrix for three-dimensional orthtropic, square symmetric, hexagonal symmetric and isotropic materials.

3.      Distinguish between elastic constants and engineering constants.

4.      For a two-dimensional orthotropic case, express and in terms of engineering constants.

5.      Derive expressions for  and  in terms of angle  and show that

                   and

      6. Assume properties given in Table 4.4 for Kevlar/epoxy and             carbon/epoxy/composites and determine [A_ij], [B_ij] and [D_ij] for a  hybrid laminate (thickness 4 mm).

      7. Make a critical assessment of various lamina failure theories.

      8. Derive expressions for Tsai-Hill and Tsai-Wu strength criteria.