(10.1)CHAPTER - 10
ENVIRONMENTAL EFFECTS
10.1 INTRODUCTION
10.2 GROUND ENVIRONMENT
10.2.1 Corrosion
10.2.2 Moisture Diffusion
10.2.3 Foreign Object Impact
10.3 SPACE ENVIRONMENT
10.3.1 Radiation and Thermo-Vacuum Environments
10.3.2 Meteororoid Environment
10.4 BIBLIOGRAPHY
10.5 EXERCISES
Composite materials and structures experience two distinct external environmental conditions (i) ground (and near ground) environment and (ii) space environment. The former is primarily dominated by the temperature and the humidity. The presence of oxygen, sodium chloride, sulphuric acid and certain other aggressive chemicals in the lower atmosphere is also of major concern. All ground based materials and structures including aircraft and other flight vehicle structural components arelikely to be affected by ground environments during their service, manufacturing and storage. The damage due to foreign body impact is also to be viewed with all seriousness, as it may lead to abort a mission or call for a major repair. The impact damage may occur owing to accidental dropping of a hard object (tool, nut, bolt, etc.) from a height. Aircraft are also quite often hit by birds (soft objects) while flying through hailstone forming clouds. The engine fans, compressor blades or the aircraft body is normally affected by such impact. The major environmental problems that are encountered by space vehicles during their flight and orbit in space are due to radiation, thermo-vacuum environment and meteoroid impact. In the present chapter we discuss some of these problems involving both ground and space environments and their effects on composite materials and structures.
Corrosion of a composite material involves the chemical or physical deterioration of its constituents (including the fibre matrix interface and the protective surface coat) when exposed to a hostile environment. Chemical degradation means weakening and/or breakage of chemical bond due to reaction of constituents with each other or the corrosive medium. The process of chemical degradation is irreversible. Physical deterioration involves only physical changes and the process is reversible. For example, the swelling of a polymer composite due to absorption of moisture is a physical degradation process, and the swelling is removed when the moisture is fully desorbed.
Corrosive environments are essentially of two types: gaseous and aqueous. The potential reactants in the gaseous environments are O2, C, Cl2 and S4 which are abundant in the ground environment. Oxidation is the most commonly observed corrosive phenomenon in a gaseous environment. Almost all metal matrices form oxides with gaseous oxygen. The rise of temperature may accelerate the oxide nucleation process. The nucleation of the oxide normally takes place at favourable sites on the metal oxygen interface. The rate of oxidation primarily depends on the physical state of oxides formed, the nature of transport processes within it and the extent of physical contact with the oxidizing environment. The oxide so formed may be solid, liquid or gaseous. A thin solid oxide layer may grow to form a thick, compact adherent scales owing to diffusion of ions through it. The formation of solid oxide scales may slow down the oxidation rate by preventing direct contact of the metal matrix with the oxygen. Liquid oxides usually flow off and volatile oxides vapourise and therefore offer little resistance to oxidation. Ceramic matrices, on the other hand possess excellent oxidation resistant properties. The oxides such as alumina, beryllia, mullite (3Al2O3 . 2SiO2), silica, titanium oxide, niclel oxide, zirconia, hafnia, ytrria and thorium oxide are more stable in air at high temperatures compared to other cermics such as nitrides, carbides or sulphides.
Carbon and glass fibres exhibit corrosion when subjected to CO and CO2 vapours. Carbon fibres are more susceptible to oxidation in presence of oxygen. Oxidation occurs on the surface and in the cracks and cavities of the fibre. The rate of oxidation is dependent on the fibre texture, inclusions, porosity and surface condition. Glass fibres with higher silica content exhibit more resistance to corrosion.
Thermoplastics, in general, possess excellent oxidation resistant properties. Oxidation of thermosets occur due to chain reactions of free radicals with oxygen that diffuses into the composite. The rate of oxidation increases with ingress of more oxygen due to a rise in temperature. It also depends on the chemical bond of different polymers. Antioxidants are normally added to reduce this type of oxidation. Oxidation results in polymer chain scissions and thereby lowering the molecular weight. Mechanical properties reduce due to a decrease in molecular weight.
Water is the most corrosive electrolyte that causes all common types of corrosion. The dissolved oxygen in aqueous solution is the major driving force to initiate corrosion at crevices that are formed by settlement of sand, debrises and marine growths on the composite surfaces or that exist in joints and other flaw sites. Pitting corrosion occurs when some localized areas are exposed due to erosion or corrosion of the protective surface layer and come in contact with aqueous solutions containing aggressive anions (strong acids) such as chlorides, bromides, perchlorates, sulphates and nitrates. However, the chloride ion is the most aggressive one. Seawater is more corrosive than natural water due to its Cl- content. Galvanic corrosion is also predominant in seawater owing to its higher electrical conductivity. Other forms of corrosion like corrosion fatigue, stress corrosion and hydrogen embrittlement are induced due to presence of applied or residual stresses.
Graphite fibre reinforced aluminium matrix (AA6061) composites exhibit accelerated corrosion when both graphite and aluminium are exposed to saline environment due to pitting, crevice corrosion or erosion of the protective aluminium surface layer. The formation of aluminium carbides at the fibre-matrix interface alters the properties of the aluminium bond layer in the affected regions and accelerates the corrosion process. The wedging of the Al(OH)3 corrosion products within the composite results in exfoliation which in turn aggravates the corrosion phenomenon. The presence of intermetallic compounds containing iron, copper, manganese and aluminium that are formed during material processing is responsible for exfoliation of the aluminium alloy (AA6061) matrix. Silicon carbide fibre reinforced aluminium composites are also affected when exposed to sea water. Pitting, both localized and distributed, is very common and the corrosion rate is relatively higher compared to graphite/aluminium composites. The discontinuous silicon carbide reinforcements (particulates or short fibres) exhibit crevice corrosion at the reinforcement-matrix interface which is responsible for subsequent excessive pitting. The corrosion of silicon carbide/aluminium composite is more severe in sea water than in marine environment.
The formation of an aluminium boride bond layer at the fibre matrix interface of boron/aluminium composite leads to corrosion at the interface. Sites containing disbands and fissures may exhibit an accelerated rate of corrosion. The fibre/matrix interface corrosion is also noticed in alumina/aluminium (AA6061) composites. On the other hand, the Li2O. 5Al2O3 bond layer in the alumina/aluminium-lithium composite prevents corrosion, when the composite is immersed in NaCl solutions. However, under such conditions, the Mg5Al8 precipitates in alumin/aluminium-magnesium composites initiates pitting at the fibre-matrix interfaces. A couple of general observations can be made based on similar studies of several metal matrix composites:
1. Most fibres and matrices corrode when exposed to a corrosive environment.
2. Erosion of protective layer, pitting and crevice corrosion accelerate the corrosion process.
3. The properties of the reinforcement/matrix interface may control the corrosion nucleation process at favourable sites.
4. The existence of disbonds, fissures, elemental segregation, inhmogeneity, nonuniform plastic deformation, cold worked regions, residual stresses, etc., may influence the corrosion process.
An appropriate protective coating, in most cases, provides a barrier between the composite and the corrosive medium and slows down the corrosion rate. Sulphuric acid anodizing and organic coatings have been found to be effective for corrosion control of graphite filament reinforced aluminium composites, whereas electroplated or vapour deposited nickel and titanium coatings may create highly unfavouable anodic (aluminium) and cathodic (nickel or titanium) area ratio at the coating flaw sites for corrosion acceleration. A surface coat of flame or arc sprayed aluminium (plus an organic top coat) may decelerate corrosion in silicon carbide/aluminium composites.
One undesirable characteristic of glass fibres is that they are soluble with either very high or very low pH level. The corrosion rate is much higher in basic solutions compared to acidic solutions. Some basic solutions such as sodium hydroxide, potassium hydroxide and sodium hypochlorite with low pH levels contain much higher hydroxyl and hydrogen ions. The corrosion of a glass fibre takes place when the negatively charged hydroxyl ions attack the positively charged silicon ions and the positively charged hydrogen ions attack the nonbridging negatively charged oxygen ions. Suitable surface treatment (sizing) is generally made to control such corrosion.
Reinforced plastic boat hulls exhibit blistering (also known as boat pox, aquatic acne or plastic plague) at the outer surfaces. The blistering is caused due to osmotic effects. An osmotic pressure builds up due to the presence of a solute within the composite, when a solvent (water or dilute sodium chloride solution) diffuses through the thin gel coat (which acts as a semipermeable membrane) and causes formation of blisters. Polyester resins which are normally used in fabrication of boat hulls contain traces of water soluble substances. Expansion of trapped gases or liquids within the voids in the composite, when exposed to hot sun, may also create differential pressure which distorts the gel coat and forms blisters. Blisters, as such, are not harmful, for they are formed on the gel coat. But their formation can activate the process of deterioration of composites due to entrapment of oxygen, water vapour and other corrosive substances within the blisters. One way to control blisters is to do away with the gel coat or use resins which do not contain solutes. The formation of microvoids is another phenomenon which is normally associated with absorption of water by polyesters and epoxies when immersed in water. These microvoids are formed as a result of chemical reactions. The swelling and plasticization of the resins occur with the absorption of moisture. Increased moisture content also results in a decrease in the glass transition temperature. The mechanical properties of composites, especially transverse and shear properties (those which are matrix-dominateed) are greatly reduced with the increase in the moisture content (Fig. 10.1). Moisture and temperature may also introduce hygrothermal stresses and deformation in laminated composite structures.
Fig. 10.1
All polymers absorb moisture in humid environment or when immersed in water. The measured critical surface tension of most polymers (18-50 dyn/cm) is lower compared to the surface tension of water (72.8 dyn/cm). All polymes are therefore hydrophobic. Diffusion is the process by which water is absorbed by a polymer. The extent of moisture absorption by a particular resin depends on the affinity of its polar functional groups for water molecules. The process of diffusion is distinctly different from the capillary action by which water is transported through fissures, cracks, voids, etc. In the case of moisture diffusion, water is not absorbed in the liquid form, but in the form of molecule or groups of molecules linked by hydrogen bond to the polymer. The absorption or desorption of moisture is governed primarily by the moisture gradients that arise due to non-uniform distribution of moisture. The transportation of mass takes place from the region of higher concentration to one of lower concentration. There are several other factors such as temperature, relative humidity, area of exposed surface, fibre and matrix diffusivities, resin content and fibre shapes that influence the moisture diffusion process.
Moisture absorption or desorption characteristics can be modeled using a simple one-dimensional form of Fick's diffusion equation
(10.1)
where C is the moisture concentration (g/m3), d22 is the diffusivity (m2/s) and t is the time (s). The Fick's relation defined in Eq. 10.1 is fundamentally equivalent to Fourier's heat conduction equation. The diffusion coefficient, d22 is a material constant and gives the measure of the rate at which moisture diffuses through the composite along the x2-axis.
Consider a semi-infinite composite body of thickness h along the x2-axis (Fig. 10.2). The boundary conditions are
C = Ci
for 0 < x2 < h when t
0
C = C0 at x2 = 0 and h when t > 0 (10.2)
Assume C0 > Ci then moisture diffuses into the composite through the faces x2 = 0 and x2 = h. The other faces are assumed to be impermeable to moisture. Let each of the faces (x2 = 0, h) has an exposed area, A, through which moisture diffuses. The solution of Eq. 10.1 is then obtained as
(10.3)
The total weight of moisture that diffuses through the two exposed faces is given by
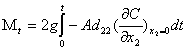(10.4)
Combining Eqs. 10.3 and 10.4 and noting that
(10.5)
one obtains Mt = 4Ag
(C0 – Ci) (d22t /
)1/2
(10.6)
The moisture content (or the percent weight gain) at a time t is given as
(10.7)
where W is the weight of the moist composite after a period of time t and Wd is the weight of the dry bone composite. Note that Wd = Ahρg with ρ is the density of the dry composites. Hence, from Eqs. 10.6 and 10.7,
(10.8)
The maximum moisture concentration within the composite reaches the level of C0 so as to be equilibrium with the outside moisture concentration (i.e., C0), when it is exposed for a long time. Hence the maximum moisture content is given by
Mm = C0 / ρ (10.9)
Substitution of Eq. 10.9 in Eq. 10.8 yields
(10.10)
Eq. 10.10 can be used to determine the diffusion coefficient d22 for a composite that permits the Fickian moisture diffusion. Figure 10.3 illustrates the moisture absorption behaviour of a typical polymer composite. In the initial phase of moisture absorption the moisture content increases linearly with the square root of the time of exposure following the Fick 's law as defined in Eq. (10.10). The diffusion coefficient, d22 is then determined from the slope as shown in Fig. 10.3, and expressed as
(10.11)
After a long exposure, the
moisture content of the composite reaches asymptotically to the maximum moisture
content, Mm. Note that the value of Mm is a material
constant, when the composite is immersed in water. When the composite is exposed
to humid environment, Mm varies with the relative humidity,
as given by
Mm
= a b
(10.12)
Where the constants a and b
(for a particular composite) are determined from the best fit curve for the Mm
vs. plot. The diffusion coefficient d11 and d33
can also be determined in a similar manner. The moisture diffusion
coefficient is normally dependent on temperature, T and can be expressed as
d = d0 exp (-A/T) (10.13)
The spatial distribution of moisture concentration, C(x2, t) at a time t can be obtained for particular boundary conditions solving Eq. 10.1 analutically (for example, see Eq. 10.3) or using the finite element method (see section 9.4) or other numerical analysis techniques. The analytical solutions are however, available for simple one-dimensional and a few two-dimensional problems. The finite element analysis technique, on the other hand, can be extended to tackle three-dimensional moisture diffusion problems and is a convenient means to solve hygrothermal (both moisture and temperature) diffusion in a composite body having complicated geometry with multidirectional fibre orientations and complex boundary conditions. The changes in the moisture concentration and temperature may introduce thermal stresses and strains in a laminate (see section 6.13). Figure 10.4 illustrate the effects of moisture concentration on the bending, free vibration and buckling of a simply supported laminated composite plate. The results are obtained using the finite element method and employing eight nodded isoparametric quadratic elements.
Fig. 10.4
Practical composites may exhibit non-Fickian diffusion behaviour. The anomalous Fickian diffusion behaviour is observed, if cracks, voids, delaminations and fibre matrix interface debonds exist in the composite and when the matrix itself exhibits non-Fickian behaviour. The existence of cracks, voids, etc., increases the moisture absorption at a faster rate. The non-Fickian behaviour of the polymer is observed when the relaxation processes inside the polymer progress at a rate comparable to the diffusion processes. The absorbed moisture may decrease the Tg thereby affecting the diffusion process. Fick's law is generally applicable to rubbery polymers, but fails to characterize the diffusion process in glassy polymers. It is, in general, observed that there exists an upper limit of humidity or temperature at which moisture diffusion deviates from that governed by Fick's law. However, much more research effort is needed to understand and analyse the effects of non-Fickian diffusion is polymer composites.
The impact considered here, is defined as the phenomenon involving collision of two elastic bodies, in which the striking object (or the impactor) has relatively less mass compared to that of the target. Examples of such impact involving composite structures (i.e., targets) are too many. A few typical examples are a bird striking an aircraft engine blade, a hailstone impacting on the aircraft wing skin, a bullet hitting a composite vest or car body panel, or a ball bounching off a composite hockey stick. The impacting velocity in these cases mostly range from Match 1 down to a few metres per second. Such an impact phenomenon is normally termed as low velocity impact. The material behaviour of the striker and the target even in the highly stressed impacting region is assumed to follow the constitutive relations defined in the realm of solid mechanics.
Consider a simple case of an elastic spherical mass impacting at the mid-span of a unidirectional composite beam (Fig. 10.5). The transverse vibrational response of the beam is then governed by the following relation:
D11W,1111 + Pw = Fc (t) (10.14)
Where Fc (t) is the time-dependent contact force exerted by the impacting mass at the contacting mid-span of the beam.
Fig. 10.5
The impactor motion is governed by
Mi wi + Fi (t) = 0 (10.15)
Where the subscript 'i' refers to the impactor.
The contact force Fe(t) during loading can be determined by the modified Hertzian contact law as given by
Fc (t) =n α3/2 (10.16)
Where α is the local indentation on the target at the contact point and n is the modified Yang-Sun contact stiffness. Note that the value of α is time dependent and it is the difference between the impactor displacement, wi and the target displacement, w at the contact point at a time t after the initial contact. The parameter n is given by
(10.17)
where,
ri is the radius of the impactor,
and Ei are elastic constants of the impactor,
and E'zz is the transverse modulus of the uppermost layer of the composite beam.
During the unloading and reloading processes the contact force is modified as
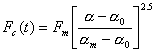(unloading) (10.18)
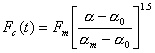(reloading) (10.19)
where Fm is the maximum contact force just before unloading, αm is the maximum local permanent indentation and α0 is defined as
α0 = 0, when αm < αcr
α0 = αm
[1- (αcr / αm ) 0.4] , when αm
αcr
(10.20)
Note that αcr is the critical indentation beyond which permanent indentation will occur.
The typical value of αcr for a carbon/epoxy composite is 8.0264 x 10-5m. The transient vibrational response problem defined in Eqs. 10.4 through 10.20 can be solved using numerical integration techniques.
Figure 10.6 shows
the impact response characteristics of a simply supported unidirectional ( =0) compositebeam (L = 0.1905m, W= 0.0127 m and h=3.175x10-5m),
when a spherical steel (Ei =210 GPa, νi = 0.3, ρi
= 7800 kg/m3) ball of 1.27 cm dia strikes the beam at the mid-span
with an initial velocity (v0) of 35 m/s. The composite properties are
assumed as follows:
E'11 = 129.207 GPa, E'22 = 9.425 GPa, G'12 = 5.157 GPa
ν'12 = 0.3, ρ = 1550 Kg/m3.
Fig. 10.6
10.3.1 Radiation and Thermo-Vacuum Environments
Figure 10.7 illustrates various regions of space. Upto an altitude of 200km from the earth's surface, the atmosphere, at an altitude of 200 km to 1000 km, is composed of atomic nitrogen and oxygen with some traces of helium between 700 km to 1000 km. High energy protons and electrons, some charged particles as well as neutral and atomic hydrogen are found at an altitude of 1000km and above. Protons and electrons may cause severe radiation damage to space vehicles because of their penetrability and higher intensity.
One of the important radiation sources for low earth orbit (LEO) satellite missions is the existence of magnetically trapped radiation consisting of electrons and protons. This radiation extends from about an altitude of 200 km to beyond synchronous orbit altitude (35, 900 km). High energy electrons are present in both the inner and outer belts tetween 5000 km to about 35,000 km. Electrons of lower energy are found at higher altitude between 40,000 km to 50,000 km. High energy protons are contained in the inner belt upto an altitude of 15000 km and lower energy protons extend into the outer belt.
Fig. 10.7
Other major prevailing radiation sources are solar cosmic rays and galactic cosmic rays. They consist of mostly protons. Solar cosmic rays are ejected sporadically from the Sun during solar flare events which at present cannot be precisely predicted. However, solar cosmic ray and galactic cosmic ray environments are hazardous for lunar and interplanetary space vehicles and for near polar or high altitude orbital missions.
Figure 10.8 describes the typical distribution of particle concentration surrounding the earth. Figure 10.9 illustrates the pressure variation upto an altitude of 800 km. it may be mentioned that as the particle concentration goes down at higher altitude, the pressure falls and vacuum is created. The pressure between 10-2 to 10-7 torr is termed as high vacuum and that from 10-8 and below is usually noted as ultra high vacuum.
Besides high or ultrahigh vacuum environment, space vehicles are also subjected to extreme temperature fluctuations. The body temperature in space is the equilibrium temperature due to direct radiation from the sun, radiation (albedo effect) from the earth and radiation by the body into space (which is a heat sink of about 4K). The body temperature is usually controlled by the materials, location of parts and thermal balance system chosen for the vehicle, and may vary between -1200C and 1500C, depending on whether the body is on the shadoe region, or it faces the sun.
Fig. 10.8
Fig. 10.9
The principal effect of radiation in polymers (both thermosetting plastics and thermoplastics) is the formation of new and irreversible chemical bonds due to cross linking between two adjacent polymer molecules. Cross linking may lead to appreciable variations in mechanical, thermal and electrical properties, as well as changes in chemical and physical states. Characteristics of these changes vary from polymer to polymer. Chain scission or fracture of polymer molecules is another phenomenon associated with radiation. This often results in decrease in Young's modulus, strength and hardness, and increase in elongation, thermal conductivity and so on.
Studies carried out to characterize effects of radiation in glasses, graphites, etc., in their bulk form, indicate that the density of most of the silica system increases with the increase of radiation and approaches a limiting value of 2200 kg/m3. The thermal conductivity of invalidated fused silica reaches a limiting value of about twice the initial value. Changes in mechanical properties such as Young's modulus, shear modulus, etc., are however less than 5 percent. The neutron irradiated graphites exhibit increase in strength, hardness and chemical reactivity, and substantial loss in thermal conductivity.
The outgassing in materials under thermo-vacuum environment is a common phenomenon. Outgassing is significant in some polymeric materials. Besides polymeric constituents, polymers contain additional substances such as solvents, catalysts, etc. Loss of gases as well as sublimation or evaporation of volatile substances occur in a high/ultrahigh vacuum environment. The process is accelerated due to elevated temperature and prolonged time of operation in such an environment. This may affect some of the important material properties such as elastic moduli, mechanical and fracture strength, coefficients of thermal expansion etc.
Meteroroid impact can cause considerable damage to space vehicles. The type and extent of damage depends on the vehicle size, structural configuration and materials, position and exposure time in space, as well as meteoroid characteristics such as velocity, density, mass flux (i.e., number of particles per unit area per unit time), and angle of impact.
Meteoroids are solid particles that are of cometory and asteroidal origin. Lunar efecta that are created by the impact of cometary particles on the lunar surface also fall under the broad category of meteoroids. Meteoroids are classified as (i) sporadics when their orbits are random, and (ii) streams or showers when most of them have nearly identical orbits.
The meteoroid environment of cometary origin is found at one astronomical unit (1AU) from the sun near the ecliptic plane. The lunar ejecta environment exists from the lunar surface to an altitude of 30 km. The meteoroid environment of asteroidal origin is commonly found in the interplanetary space, particularly in the asteroidal belt between Mars and Jupiter. In the near-earth region (1AU) asteroidal particles are assumed to be non-existent and hence particles of cometary origin are of major concern.
The cometory meteoroid is porous, highly frangible and often described as dust ball or a conglomerate of dust particles bound together by frozen gases/ices. The particle mass ranges from 10-12 to 1 gm for sporadic meteoroids and 10-6 to 1 gm for stream meteoroids. The mass density is assessed to be about 0.5 gm/cm3. The geometric velocity varies between 11 and 72 km/sec. An average atmospheric entry velocity of 20 km/sec is assumed as the average velocity of sporadic meteoroids. The velocity of stream meteoroids varies from stream to stream. For example Leonid has a stream velocity of 72 km/s, while the velocity of Bielids is 16 km/s, although both appear during the month of November. An average total meteoroid (average sporadic plus a derived average stream) environment can be assumed in the initial design phase. This average cumulative meteoroid flux-mass model is expressed as
10-6
m 100 : log10 N = -14.37 –
1.213 log10 m
10-12 m 10-6 : log10 N = -14.339 –
1.584 log10 m
– 0.063 (log10m)2 (10.21)
where
N = number of particle of mass m or greater per square meter per second
m = particle mass in grams.
The following Poisson distribution equation describes the probability of impact by meteoroids.
(10.22)
where
= probability of impact by n meteoroids or less
N = flux, particles/m2 as defined in Eq. 10.21
(accounting for the effects of gravitational focusing and of shielding by planetary bodies or by the parts of the vehicle, if applicable).
A = exposed area, m2
t =exposure time, second
The flux-mass relations given in Eq. 10.14 and Eq. 10.15 should be used to establish the probability of impact by n or less meteoroids of a particular mass or greater.
When a meteoroid hits a target in the hypervelocity range1, the following phenomenon occurs. An enormous shock pressure is built up at the interface between the target and projectile. This causes the material at the point of contact to be compressed almost instantaneously to an extremely high pressure. Fracture occurs when the stress exceeds a critical value. As the shock passes through the target, the pressure decreases rapidly and the material expands adiabatically. This process creates irreversible shock heating which may even lead to fusion, liquefaction and vapourisation. As the shock pressure propagates away, its intensity reduces. Then the pressure fails below the strength of the material and the damage is arrested. However, for a brittle target, the initial damage may lead to catastrophic failure.
The response of a structure under meteoroid impact depends primarily on the structure material, thickness, type of construction (laminated, sandwich, etc.) and temperature as well as the meteoroid characteristics.
Foot Note 1: Subordinate range : 25 to 500 m/s
Nominal ordance range : 500 to 1300 m/s
Ultraordnance range : 1300 to 3000 m/s
Hypervelocity range : >3000 m/s
Both experimental studies and analytical studies have been carried out to assess the damage due to the simulated meteoroid impact on metallic targets. The experimental study involves use of particle accelerators. The pellet materials are aluminium and glass. Syntactic foam (hollow glass spheres embedded in plastic matrix) has also been used as a pellet with the density as low as 0.7 gm/cm3. Two major limitations of experimental studies are : realization of higher velocity and simulation of the desired range of meteoroid density.
Analytical method employ incompressible and compressible hydrodynamic theories that provide excellent understanding of the penetration of hypervelocity particles. In the former case, large stresses developing due to the hypervelocity impact permit neglect of rigidity and compressibility of striking bodies and the impact is viewed as fluid flow. This simplifies the description of material properties to a great extent. The refined analyses consider materials to be compressive fluids and also take into account effects of material strength.
The results of impact damage phenomenon in composites, that are available in the open literature, mostly relate to FCD (Foreign Object Damage). Both analytical and experimental investigations have been carried out to study the transient and steady state responses and damage mechanics. However, these results are not applicable to meteoroid impact as the foreign object impact velocity considered in these studies fall well below the hypervelocity range. Hence there is considerable need to investigate and identify the impact damage mechanics in composites in the hypervelocity range and to establish appropriate methodology for design of composite structural elements against hypervelocity impact.
1. W. K. Bond and F.W.Fink, Corrosion of Metals in Marine Environments, Metals and Cermamics Information Centre,OH, 1978.
2. C.R. Crowe, Localised Corrosion Currents from Gr/Al and Welded SiC/Al Metal Matrix Composites, NRL Report 5415, 1985.
3. P.P. Trzasloma, The Corrosion Behaviour of a Graphite Fibre/Magnesium Metal Matrix in Aqueous Chloride Solution, NRL Report 5640, 1985.
4. D.M. Aylor, Metal Matrix Composites: Corrosion, in International Encyclopedia of Composites (S.M. Lee, Ed.), Vol. 3, VCH, NY, 1990, p.228.
5. P. Schweitzer (Ed.), Corrosion and Corrosion Protection Handbook, Marcel Dekker, NY,1983.
6. W. Schnabel, Polymer Degrdation : Principles and Practical Applications, Macmillan, NY, 1988.
7. J.H.Mallinson, Corrosion-Resistant Plastic Composites in Chemical Plant Design, Marcel Dekker, NY, 1988.
8. G.S. Springer (Ed.), Environmental Effects in Composite Materials, Vols. 1-3, Technomic Publ. Co. Inc., Lancaster, 1981, 1984 and 1988.
9. B.C. Ray, A. Biswas and P.K. Sinha, Freezing and Thermal Spikes Effects on ILSS values of Hygrothermally Conditioned Fibre/Epoxy Composites, J. Materials Science Letters, 11, 1992, p. 508.
10. P.K. Aditya and P.K. Sinha, Diffusion Coefficient of Polymeric Composites Subjected to Periodic Hygrothermal Exposures, J. Reinforced Plastics and Composites, 11, 9, 1992, p. 1035.
11. P.K. Aditya and P.K. Sinha, Effects of Fibre Shapes on Moisture Diffusion Coefficients, J. Reinforced Plastics and Composites, 12, 9, 1993, p. 973.
12. P.K. Aditya and P.K. Sinha, Effects of Arbitrarily Shaped Fibres on Moisture Diffusion Coefficient of Polymeric Composites, J. Reinforced Plastics and Composites, 13, 2, 1994, p. 142.
13. P.K. Aditya and P.K. Sinha, Effects of Fibre Permeability on Moisture Diffusion Coefficients of Polymeric Composites, Polymers and Polymer Composites, 1, 5, 1993, p. 341.
14. P.K. Sinha, Failure of Composites, Report No. AEM-H1-20, Department of Aerospace Engineering and Mechanics, Univ. of Minnesota, MN, 1978.
15. P. K. Sinha, A Review of Moisture Diffusion in Composites, Report No. AEM-H1-19, Department of Aerospace Engineering and Mechanics, Univ. of Minnesota, MN, 1978.
16. J.S. Carslaw and J.C. Jaegar, Conduction of Heat in Solids, Clarendon, Oxford, 1959.
17. W. Jost, Diffusion in Solids, Liquids and Gases, Academic Press, 1960.
18. J. Crank, Mathematical Theory of Diffusion, Oxford Press, London, 1975.
19. K.S. Sai Ram and P.K. Sinha, Hygrothermal Effects on the Bending Characteristics of Laminated Composite Plates, Computers and Structures, 40, 1991, p. 1009.
20. K.S. Sai Ram and P.K. Sinha, Hygrothermal Effects on the Free Vibration of Laminated Composite Plates, J. Sound and Vibration, 158, 1992, p. 133.
21. K.S. Sai Ram and P.K. Sinha, Hygrothermal Effects on the Buckling of Laminated Composites Plates, Int. J. Composite Structures, 21, 1992, p. 233.
22. R.B. Hetnarski (Ed.), Thermal Stresses, I and II, Elsevier, Amsterdam, 1991.
23. Space Radiation Protection, NASA SP 8054, 1970.
24. D. J. Santeler et al., Vacuum Technology and Space Simulation, NASA SP 105, 1967, p. 197.
25. Nuclear and Space Radiation Effects on Materials, NASA SP 8053, 1970.
26. J. Bourriean and A. Paillous, Effect of Radiations on Polymers and Thermal Control Coatings, ESA SP-145, 1979, p. 227.
27. R. C. Tennyson, Composite Materials in a Simulated Space Environment, AIAA Paper No. 80-0678, 1980.
28. R. C. Tennyson et al., Space Environmental Effects on Polymer Matrix Composites, ESA SP-145, 1979, p. 263.
29. Meteoroid Environment Model – 1969 (Near Earth to Lunar Surface), NASA SP-8013, 1969.
30. W. Goldsmith, Impact, Edward Arnold (Publishers)Ltd., London, 1960.
31. A.C. Eringer, Transverse Impact on Beams and Plates, J. Applied Mechanics, Trans. ASME, 72, 1950, p. 461.
32. E. H. Lee, The Impact of a Mass Striking a Beam, J. Applied Mechanics, Trans. ASME, 62, 1940, p. A67.
33. M.E. Backman and W. Goldsmith, The Mechanics of penetration of Projectiles into Targets, Int. J. Engng. Sci., 16, 1978, p.1.
34. A.J. Cable, High Velocity Impact Phenomena, Academic Press, NY, 1970.
35. Meteoroid Damage Assessment, NASA SP-8042, 1970.
36. Foreign Object Impact Damage to Composites, ASTM STP 568, 1975.
37. F.C. Moon, Wave Propagation and Impact in Composite Materials, Composite Materials, (Eds. L.J. Broutman and R.H. Krock), Vol. 7, Part I, Academic Press, NY, 1975, p. 260.
38. W.S. de Rosset, Fracture of Boron Epoxy Composite due to Impact Loading, J. Composite Materials, 9, 1975, p. 114.
39. J. Awerbuch and H. T. Hahn, Hard Objet Impact Damage of Metal Matrix Composites, J. Composite Materials, 10, 1976, p. 231.
40. C. T. Sun, Propagation of Shock Waves in Anisotropic Composite Plates, J. Composite Materials, 7, 1973, p. 366.
41. Y. Oved and G. E. Luttwak, Shock Wave Propagation in Layered Composites, J. Composites, J. Composite Materials, 12, 1978, p. 84.
42. S. H. Yang and C. T. Sun, Indentation Law for Composite Laminates, NASA CR-165460, 1981.
43. C.T. Sun and J.K. Chen, On the Impact of Initially Stressed Composite Laminates, J. Composite Materials, 19, 1985, p. 490.
44. D.S. Cairrons and P.A. Lagace, A Consistant Engineering Methodology for the Treatment of Impact in Composite Materials, J. Reinforced Plastics and Composites, 11, 1992, p. 395.
45. N. Y. Choi and F. K. Chang, A Model for Predicting Graphite /Epoxy Laminated Composites Resulting from Low-Velocity point Impact, J. Composite Materials, 62, 1992, p. 2134.
46. D.K. Maiti and P.K. Sinha, Impact Behaviour of Thick Laminated Composite Beams, J. Reinforced Plastics and Composites, 14, 1995, p. 255.
47. D.K. Maiti and P.K. Sinha, Bending, Free Vibration and Impact Response of Thick Laminated Composite Plates, Computers and Structures (Communicated).
48. D.K. Maiti and P.K. Sinha, Finite Element Impact Analysis of Doubly Curved Laminated Composite Shells, J. Reinforced Plastics and Composites (communicated).